Rectas Paralelas Secantes Y Perpendiculares Para Niños De Primaria – Iniciando con Rectas Paralelas, Secantes y Perpendiculares para Niños de Primaria, este párrafo inicial está diseñado para cautivar y atraer a los lectores, estableciendo un tono académico con estilo autoritario que se despliega con cada palabra.
El contenido del segundo párrafo proporciona información descriptiva y clara sobre el tema.
Definición y características de las rectas paralelas, secantes y perpendiculares
Las rectas son líneas rectas que se extienden indefinidamente en ambas direcciones. Pueden tener diferentes relaciones entre sí, como ser paralelas, secantes o perpendiculares.
Rectas paralelas
Las rectas paralelas son líneas rectas que nunca se cruzan, no importa cuán lejos se extiendan. Siempre mantienen la misma distancia entre sí. Por ejemplo, las vías del tren son rectas paralelas.
Rectas secantes, Rectas Paralelas Secantes Y Perpendiculares Para Niños De Primaria
Las rectas secantes son líneas rectas que se cruzan en un solo punto. Por ejemplo, las diagonales de un rectángulo son rectas secantes.
Rectas perpendiculares
Las rectas perpendiculares son líneas rectas que se cruzan en un ángulo recto (90 grados). Por ejemplo, los lados de un cuadrado son rectas perpendiculares.
| Tipo de recta | Definición | Propiedades |
|---|---|---|
| Paralela | Líneas rectas que nunca se cruzan. | Mantienen la misma distancia entre sí. |
| Secante | Líneas rectas que se cruzan en un solo punto. | Forman ángulos distintos de 90 grados. |
| Perpendicular | Líneas rectas que se cruzan en un ángulo recto (90 grados). | Forman cuatro ángulos rectos. |
Propiedades de las rectas paralelas: Rectas Paralelas Secantes Y Perpendiculares Para Niños De Primaria
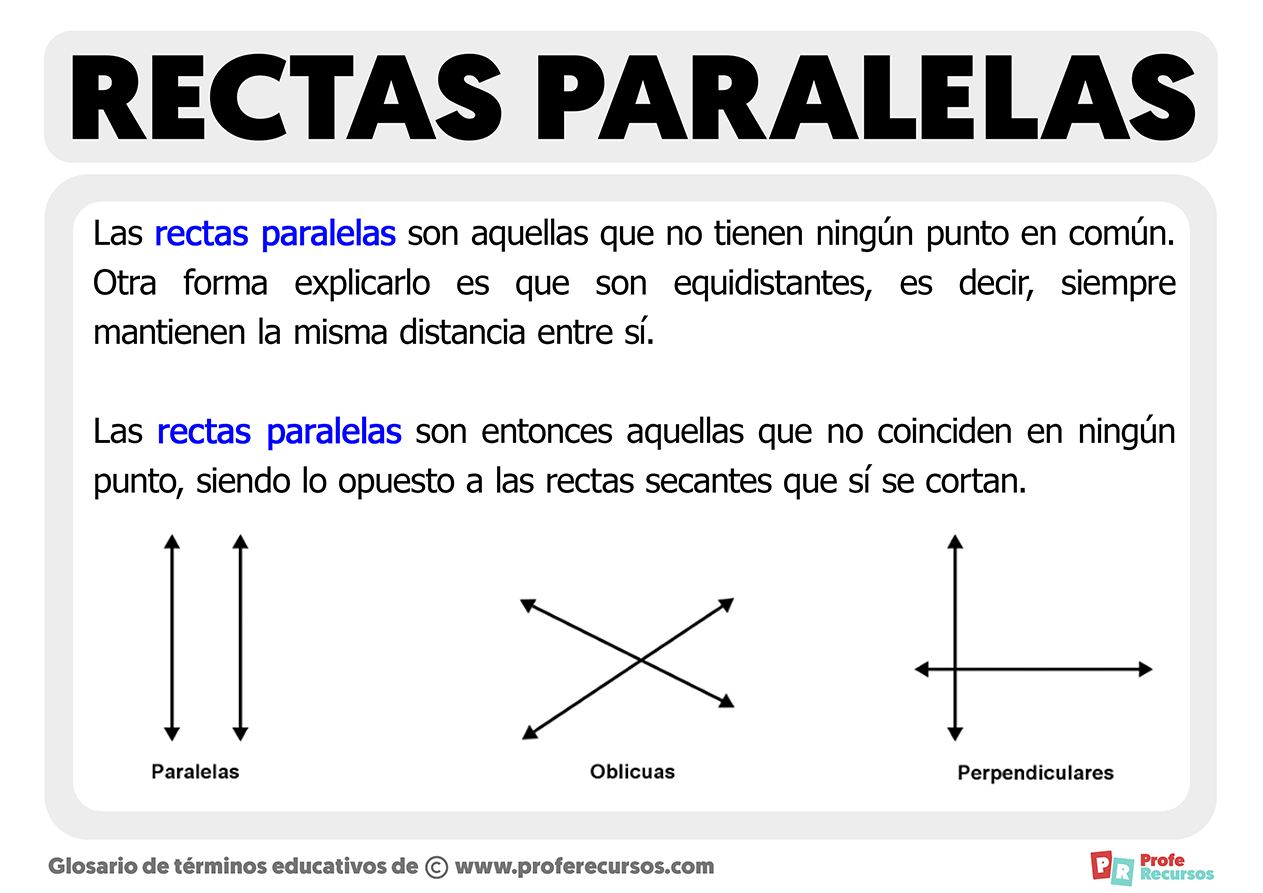
Las rectas paralelas son rectas que nunca se intersectan, sin importar cuánto se extiendan. Son equidistantes entre sí, lo que significa que la distancia entre ellas es siempre la misma.
Ejemplos de rectas paralelas
- Los rieles de un tren
- Los lados opuestos de un rectángulo
- Las líneas de un papel pautado
Actividades prácticas para demostrar las propiedades de las rectas paralelas
- Usa dos reglas o palos para representar rectas paralelas. Muestra que nunca se cruzan.
- Dibuja dos líneas paralelas en una hoja de papel. Mide la distancia entre ellas en varios puntos. Demuestra que la distancia es siempre la misma.
- Construye un modelo de una casa con dos paredes paralelas. Usa un hilo para conectar las dos paredes y muestra que el hilo siempre está a la misma distancia de ambas paredes.
Propiedades de las rectas secantes
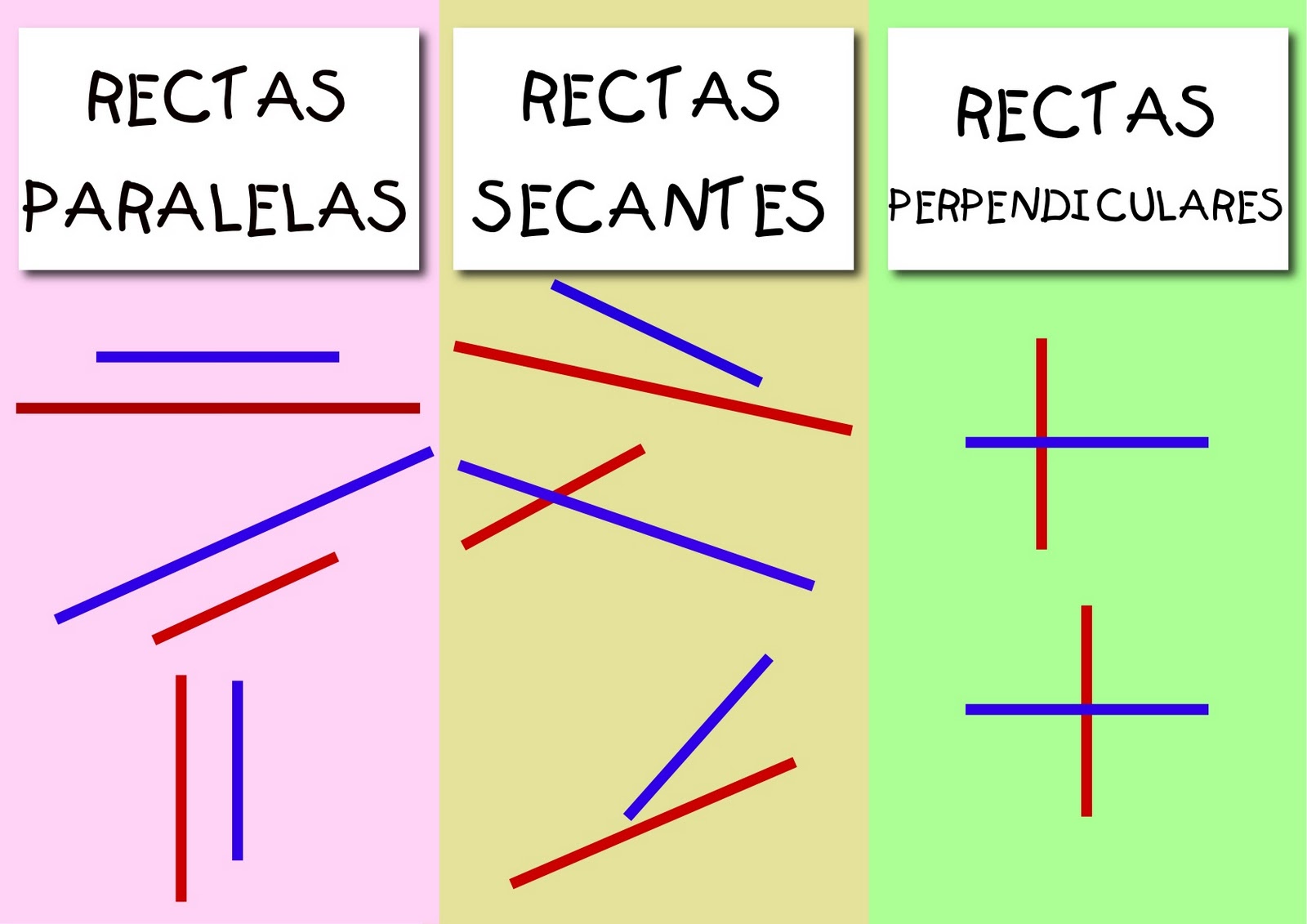
Las rectas secantes son aquellas que se cruzan en un punto, formando ángulos.
Intersección de rectas secantes
Cuando dos rectas secantes se cruzan, forman cuatro ángulos: dos ángulos opuestos por el vértice y dos ángulos adyacentes. Los ángulos opuestos por el vértice son iguales, mientras que los ángulos adyacentes son suplementarios (suman 180 grados).
Ejemplos de intersecciones de rectas secantes
En la vida real, las rectas secantes se pueden encontrar en situaciones como:
- El cruce de dos calles
- El encuentro de dos líneas de ferrocarril
- La intersección de dos tuberías
Diagrama de flujo para identificar y clasificar las rectas secantes
Para identificar y clasificar las rectas secantes, podemos seguir el siguiente diagrama de flujo:
¿Las rectas se cruzan?
Sí
rectas secantes
No
rectas no secantes
¿Las rectas se cruzan en un punto?
Sí
rectas secantes simples
No
rectas secantes compuestas
¿Las rectas forman ángulos iguales?
Sí
rectas secantes perpendiculares
No
rectas secantes oblicuas
Propiedades de las rectas perpendiculares
Las rectas perpendiculares poseen propiedades únicas que las distinguen de otros tipos de rectas. Estas propiedades se pueden observar en varios objetos de nuestro entorno y pueden demostrarse mediante experimentos sencillos.
Intersección en ángulo recto
Una de las propiedades más importantes de las rectas perpendiculares es que se intersecan en un ángulo recto. Esto significa que forman un ángulo de 90 grados cuando se cruzan. Esta propiedad es esencial para muchas aplicaciones prácticas, como la construcción y la medición.
Formación de segmentos congruentes
Cuando dos rectas perpendiculares se intersecan, forman cuatro segmentos congruentes. Estos segmentos son iguales en longitud y se encuentran en los lados opuestos del punto de intersección. Esta propiedad es útil para verificar la perpendicularidad de las rectas y para realizar mediciones precisas.
Ejemplos de rectas perpendiculares en el entorno
- Los bordes de un cuadrado o rectángulo
- Los lados opuestos de un cubo
- Las líneas divisorias en un campo de fútbol
Experimentos sencillos para demostrar las propiedades de las rectas perpendiculares
- Experimento 1:Coloca dos reglas una encima de la otra formando una cruz. Observa que las reglas se intersecan en ángulo recto y forman segmentos congruentes.
- Experimento 2:Dibuja dos líneas paralelas en una hoja de papel. Luego, dibuja una línea perpendicular a una de las líneas paralelas. Mide los ángulos formados por la línea perpendicular y las líneas paralelas. Deberías obtener dos ángulos rectos.
FAQ Guide
¿Qué son las rectas paralelas?
Son rectas que nunca se cruzan, por más que se extiendan.
¿Qué son las rectas secantes?
Son rectas que se cruzan en un solo punto.
¿Qué son las rectas perpendiculares?
Son rectas que se cruzan formando un ángulo recto (90 grados).
